You can’t put the number 2 next to the number 1.
Try not one, but two maths games! These games will help you create mathematical networks revealing underlying pattern.
You will need
- A printout of the two game boards
- 8 counters numbered 1-8
What to do
- Put the counters on game board 1 so that consecutive numbers are not next to each other – across, up, down, or diagonal.
The number 2 must be connected to the number 1.
- Now put the counters on game board 2 so consecutive numbers are joined by lines
Which one was easier?
What’s happening?
It may seem odd, but the two questions are the same. If you put numbers on the same letters each time, a solution for game 1 is also a solution to game 2 and vice-versa.
Game 2 was constructed from game 1. If two boxes are not next to each other in game 1, a line is drawn between them in game 2. If there is no line between two boxes in game 2, then they must be next to each other in game 1.
The first game has you looking for things that are far away from each other. It is not hard, but it is hard enough that you can’t see patterns very easily. In Game 2, the relations between squares are obvious lines. This makes it a lot easier to look at the underlying pattern.
Real-life maths
Drawing a network like the second puzzle emphasises the links between the squares, rather than the squares themselves. This can be very useful in many areas of study, including manufacturing, route planning, and ecology.
Ecologists use networks to represent how different animals interact in the environment. Often the links represent one animal eating another, but other important links exist. For example, bees are necessary for some plants to reproduce.
Mathematicians can study these networks and identify interesting loops in the links. Some loops take small changes in a population and make them larger. Other loops can be very stable, and will work to fix any change in animal populations. Small changes can also have flow on effects, causing significant changes in completely different species.
Scientists also use these networks to design mathematical models of how animal populations interact. These models can predict what might happen if an animal became extinct, or if a new animal was introduced.
Studies of ecological networks have been used to solve problems in ecosystems. In Scotland, scientists are planning to re-introduce wolves to reduce deer populations.
If you’re after more maths activities for kids, subscribe to Double Helix magazine!




2 responses
This comment is about the Unfriendly Neighbours activity. Is there a typo in the instructions perhaps? In step 1, consecutive numbers should not be beside one another. In step 2, consecutive numbers must be linked. I thought it was meant to be 2 formats for the same puzzle. I don’t understand how these 2 activities achieve the same thing. In the first puzzle the numbers have 5 or 6 possible options to choose as their non-consecutive neighbor. In the second puzzle, the numbers have only 1 or 2 options for their consecutive neighbor. Could you please explain?
Hi Mike,
Thanks for your question! I’m pretty sure the activity is all right. It’s a bit tricky to get though, so I’ll see if I can explain it a bit better.
The idea is that it’s actually kinda hard to see which boxes aren’t close together. It’d be much easier if those boxes were, say, connected with lines.
That’s what we’re doing. Check the matching letters here:
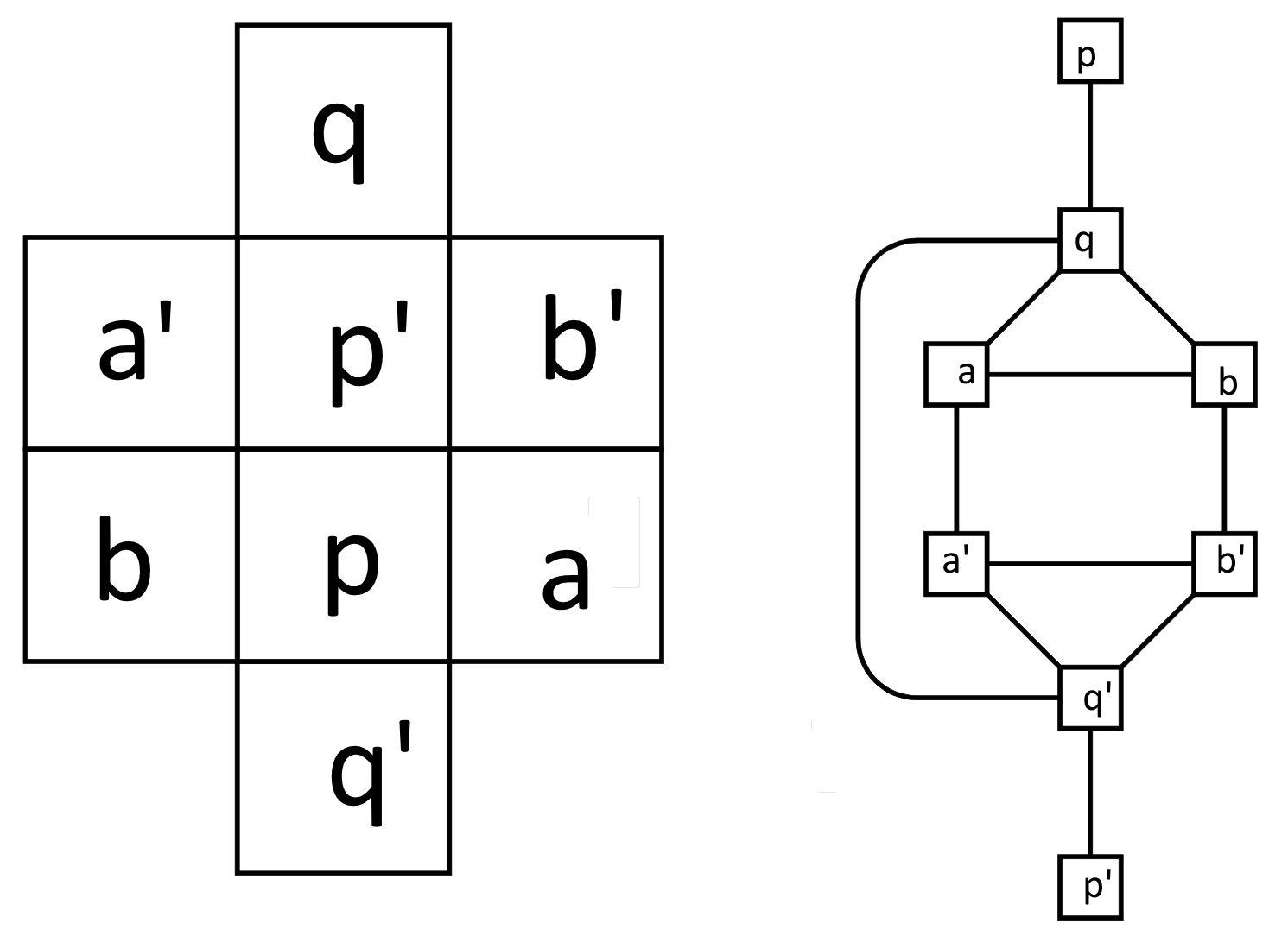
If two boxes are NOT adjacent on the first, they ARE connected in the second.
To a mathematician, the questions are essentially the same. Because mathematicians are a bit weird.
Anyways, hope this helps!
By submitting this form, you give CSIRO permission to publish your comments on our websites. Please make sure the comments are your own. For more information please see our terms and conditions.